本系列分为两部分,本文是第二部分。
流浪猪
第二部分 圣维南多项式 估计河流和海面线 1 圣维南多项式
描述江河圣维南多项式的方法有很多种,它们的数学意义是相同的。 本文选取其中之一作为[1]:
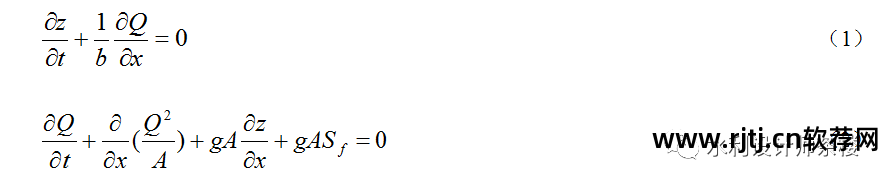

2 几个重要概念 2.1 差分方案及其解概述
由方程(1)和(2)组成的常微分多项式的数值解大多采用差分法[2]和有限体积法[3]。 一些高精度格式。 很多学者也将有限体积法纳入差分法中,我们也将其纳入讨论。
差分多项式有更多的差分格式,赋予它们不同的代数精度。 用于圣维南多项式的微分格式也应该是守恒型[2]微分格式,满足水量和动量守恒; 它具有输运特性[2],可以反映水体积和动量的输运特性。
圣维南多项式群是非线性多项式,一般需要转化为线性多项式群进行迭代求解; 每次迭代中转换的线性多项式组大多通过追踪法(TDMA算法)求解[3]。
2.2 收敛性与稳定性
只有差分多项式收敛才能得到合理可行的解。 差分格式和多项式群解是决定收敛性的两个关键因素。 收敛性和稳定性是互为充分且必要的条件。 能量多项式可以被视为恒流圣维南多项式的特例。 能量多项式的稳定性在第一篇文章中已经讨论过,读者也可以作为本文的参考。 一般来说,隐式格式是无条件稳定的,显式格式是有条件稳定的[4]。
2.3 耗散和色散
耗散[2]是指差分多项式与常微分方程组的倍数比,色散[2](俗称色散)是指差分多项式与常微分方程组的相位比。 形象地说,耗散往往会引起突变程度和幅度的变化,比原来的多项式突变更强烈或更慢; 色散常常在图形突变附近形成一些虚假振荡。 耗散和色散都是数值估计造成的偏差,甚至是原来的常微分多项式不存在的现象,是数值估计形成的独特现象。
2.4 边界条件
圣维南多项式差分后,多项式数量多于未知数数量,需要引入边界条件来求解问题。 对于进、出口边界,一般上游入口已知流量,下游出口已知水位或水位流量关系; 每个估计部分还具有后流入; 本文将系统与周围环境的关系称为外边界。 对于系统来说,可能存在桥梁、堰、消力池、调节池等设施,它们控制着系统的运行,对系统起到控制作用。 本文将其命名为内边界。 对于非定常流(俗称不稳定流)来说,它属于非线性演化多项式,任意时刻的流动状态与初始状态密切相关,因此必须提前给出初始流动状态,以便将其与上述两个边界条件,本文称为初始边界条件(或初始状态)。
2.5 估算周期的选择

2.6 总结
对于微分多项式,要注意守恒、输运、稳定性、耗散和色散五个性质。 因为大多数工程师使用成熟的商业软件来估算,一般来说,保存、运输、稳定性都没有问题; 如果需要高精度冲击波捕获,则必须仔细选择差分格式以保持良好的耗散和色散特性; 对于非高精度激波捕获的一般估计,只需对耗散和色散有正确的认识,对数值估计偏差的欺骗有一定的抵抗力即可。
构建模型时,需要谨慎处理边界条件。 初学者往往对模型的构建非常认真,但遗憾的是定性边界条件粗心且简单,导致估计结果与事实相差很大。 鉴于大多数工程师使用成熟的商业软件来估计实际情况渠道水面线计算软件,本文将重点介绍一些非定常流边界条件的示例。
3 稳流 3.1 方程及特性

3.2 与能量多项式的关系及比较
由式(3)的区别不难看出,在稳定流中,任意断面的流量都是上游流入量与所有后方流入量之和。 (4)式的差值可以转化为不考虑局部水头损失的能量多项式。 St. Venant多项式法与能量多项式法在稳定流海面线估算方面没有本质区别,而且由于St. Venant多项式法与能量多项式法相比,精度有所欠缺。
对于环形沟渠、支流河道等特殊路堤,稳定流圣维南多项式法可以一次性求解,而能量多项式法则需要多次试验才能计算分流比。 这时,稳流圣维南多项式法就具有了较大的优势渠道水面线计算软件,该方法可以减少能量多项式法大量试算的工作量。
对于能量多项式法,需要给出每个估计断面的流量。 对于圣维南多项式法,需要给出上游入口断面的流量和每个估计断面的前侧流入量。 需要注意的是,由于圣维南多项式法任意断面的流量都是其上游入流与所有后方入流之和,因此必须根据该断面上下游断面的设计流量乘以后方入流。估计河流断面。 如果背面入流直接采用同频区间洪峰,会虚减各断面的设计流量,导致海面线结果偏低且畸变严重。 沟渠各断面洪峰出现时间不同,能量多项式法和稳流圣维南多项式法大多采用各断面流量峰值,较为保守。
因此,不能盲目采用恒流圣维南多项式法,非必要时应尽量采用能量多项式法。
4 非定常流动 4.1 Preissmann隐式差分格式
本文所举的非定常流例子采用了Preissmann隐式差分格式,下面对此进行介绍。 圣维南多项式差分和拟牛顿化可以重写为[1]:
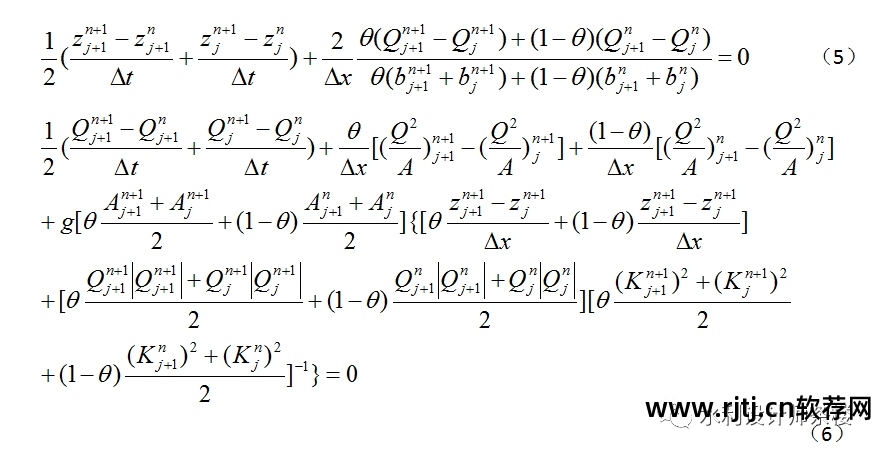

4.2 边界条件设置部分工程实例介绍
在大多数工程师依赖成熟商业软件进行估算的实际情况下,很少有人像笔者一样自己编程估算,所以下面给出一些边界条件的例子供参考。 对详细案例感兴趣的读者可以参考相关论文。
1.青山河水电站隧道式前池涌浪模拟[5]
青山河水电站位于广东省石台县七井乡青山河上,校址位于石台县七井乡水草河上。 电厂引水系统由渠道、隧道、压力铁管三部分组成; 其中,隧道全长2584.2m。 、局部拱圈、坝体断面侧墙、顶拱混凝土坝体厚度0.25m,混凝土底板厚度0.2m; 隧道尽头为隧道式前池,隧道式前池总长49.2m,分为四段。 第一段为陡坡地段,长24m,底板标高由332.41增加到327.57m,洞体尺寸由1.5×1.8m增加
改为3.5×7.55m; 第二段为3m长沉砂池段,沉砂池深度为1.0m; 第三段为长12m的池体,洞体尺寸为3.5×6.55m; 第四段为溢流堰段,长10.2m,坝顶高程333.37m。
浪涌模拟包括最大正浪涌和最大负浪涌。 当设备突然卸下所有负载时,会出现最大正浪涌。 可以通过在孤立运行的水电站中突然增加一台发电机组来估计负浪涌。
(一)模型情况
青山河水电站隧道及前池定义为171个断面进行估算,除前池陡坡段长24m外,其余断面均取15m,估算断面总长2574m。 模型入口为隧道入口(洞体),出口位于前池溢流堰(洞体)前。 无衬砌隧道断面粗糙度n=0.035,坝体断面粗糙度n=0.017,Δt=5s。
(2) 最大正浪涌波的边界条件
1、初始边界条件:导流明渠前湾系统在设计流量(1.581m3/s)下为恒流(末端水位333.37m);
2、外部边界条件:上游水稳定注入隧道,上游边界条件为已知流量(Q=1.581m3/s)
边界条件; 下游边界条件是已知水位-流量关系的边界条件。 当出现正涌时,所有机组在导叶事故停机时间(5s)内从满流量减至零,当水位低于堰顶时,泄水时,堰流量为自由流量。流量,堰上水头与流量的关系为
(3)负浪涌边界条件
1、初始边界条件:引水渠前池系统在满足一单位配水量所需的超额流量(0.527m3/s)的条件下为恒流(配水前的超额流量被前池溢流)溢流堰)。
2、外边界条件:上游边界条件为已知流动条件,初始条件流入量保持不变; 当前池水位低于溢流堰顶时,下游边界条件为已知水位-流量关系条件,即水位取决于发电总流量与通流能力之和溢流堰; 当前池水位高于溢流堰顶时,下游边界条件为已知流量条件(总发电流量)。
2.龙津河纳提德 [6]
龙津河位于广州省阳西县境内。 发源于莲花山,自西南向东南纵贯市区。 经拉萨水库流入杭州湾,出口受拉萨水库控制。 那超河段自城市青年景区皮头至出口拉萨水库,全长约14Km,河底高程约-2.0~-2.5m。 当潮水位高于0m时,通过大沥水库泄水,当潮水位低于0m时,通过大沥水库受潮,加速堤坝的沉积并改善水质。
(一)模型情况
潮沟总长14Km,共划分15段,段宽约1Km。 拉萨水库以宽顶堰流为内边界,△t=120s。
(2) 初始边界条件
收潮主要发生在旱季。 考虑到受潮初期堤岸仍为积水,各估算断面流量取0m3/s,水位0m。
(3)外部边界条件
由于控制流域面积较小,枯水期不考虑上游水流,上游边界条件为已知水流条件,流量为0m3/s; 拉萨水库下游是已知水位,即潮位过程。
3、乌坎水库泄洪[7]
乌坎水库位于广州省化州市金乡镇王窑村。 距萨哈林岛约3公里。 水库下游堤坝宽约300-400m。 。 乌坎水库的防洪原则是:当水库水位为0m时,闸门水位为0m,按来水泄洪。 随着来水的减少,闸门的开度逐渐增大,直至闸门完全打开,闸门内的水位开始下降; 当闸内水位低于0m且低于下游水位时,尽力泄洪; 当潮位下降,使水闸下游水位低于上游水位时,水闸关闭挡潮。
(一)模型情况
采用乌坎水库作为水平衡多项式防洪模型; 乌坎水库下游3公里处分为四段,段宽约1公里。 洪水调节多项式和圣维南多项式通过水库下游断面的水位和流量进行耦合。 水库下游断面(圣维南多项式最上游断面)水位影响水库流量估算的吞没系数,调洪流量成为圣维南多项式上游入流条件。
(2) 初始边界条件
水库上游库区水位0m,泄流量0m3/s。 各断面流量为0m3/s,水位为当时对应的潮位。
(3)外部边界条件
如果将防洪多项式视为耦合圣维南多项式的一部分,并用形式防洪多项式作为圣维南多项式的内边界条件,则上游边界条件为已知流量条件,即是,门口现场大雨; 如果分别处理洪水调节多项式和圣维南多项式,则上游边界条件为已知水流条件,即水库泄流流量。 下游边界条件为已知水位,即潮位过程。
参考:
[1]鞠江. 工程水力学数值模拟与可视化[M]. 上海:中国水利水电出版社,2010。
[2] 张德良. 估计流体热程[M]. 上海:高等教育出版社,2010。
[3] 李仁贤. 有限体积法基础[M]. 上海:国防工业出版社,2008。
[4] 郑先义,姚养新,雷秀仁,等。应用数值分析[M]. 上海:华东理工大学出版社,2008。
[5]王志,周斌。 基于圣维南多项式的青山河水电站隧道式前池涌浪模拟[J]. 湖南水利科学技术,2019(2)。
[6]周斌,张彦军. 基于潮汐的龙津湖水体更新模拟与分析[J]. 人民珠江,2015(3)。
[7]周斌,黄松莲。 潮汐河堤、湖泊水闸防洪计算方法研究[J]. 人民珠江,2016(1)。
供稿:周斌(潮州市水利水电规划设计院副院长)

