【新智慧入门】近日,微软的研究人员开源了一个使用新方法训练的大型MoE模型,该模型不同寻常,具有出色的编码和数学性能。
继Phi家族之后,微软又开源了一个新的大型混合专家模型——GRIN MoE。
与Phi-3.5(16 * 3.8B)大小相同,但采用完全不同的训练方法。
如果这句“不走寻常路”太长,写不下去的话,那就是两句话:
1.使用新一代SparseMixer精确估计专家路由的梯度,解决传统方案中使用门控梯度代替路由梯度的问题。 2.不再需要专家并行性。相反,在训练中使用数据、管道和张量并行,这避免了传统方法中丢弃标记的问题。

论文地址:
当然,上面两句话是小编说的,有点粗糙。详细内容请继续阅读文章~
如今,如果你是LLM新手,当然首先要提高你的分数——
参数要少,效果要好,所以应该在左上角:

作为MoE架构,GRIN的总参数量约为42B,推理时激活的参数为6.6B。同级别(7B)的非 MoE 型号很容易获得,甚至比 14B Phi-3 稍好一些。
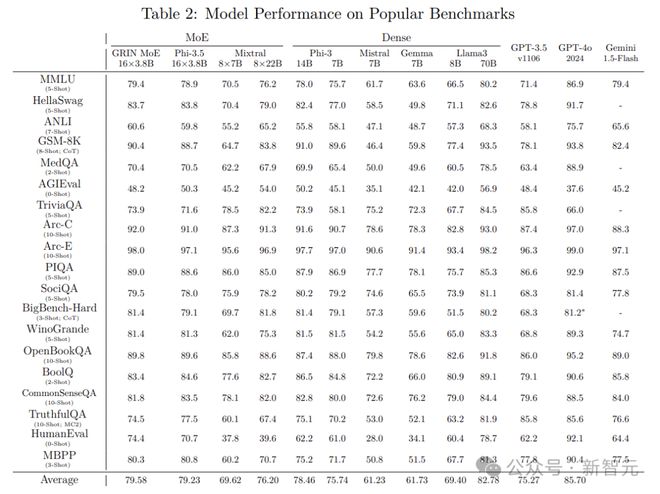
在上面的成绩单中,GRIN MoE 表现出色,尤其是在编码和数学测试方面。
例如,在衡量数学问题解决能力的GSM-8K中,GRIN MoE得分为90.4,在编码任务基准Humaneval上得分为74.4。
在MMLU(大规模多任务语言理解)基准测试中,GRIN 得分为 79.4,超过了同为 MoE 架构的 Mixtral(70.5 分)以及其自身的 Phi-3.5(78.9 分)。
如果与流行的商业模式相比,GPT-3.5意味着感受时代的力量,默默退出群聊。

开放重量:
演示:
教育部新培训路径
GRIN MoE由规则的Transformer块组成,并采用分组查询注意力(GQA)和滑动窗口注意力来提高计算效率。
RoPE用于位置编码,以在预训练后实现长上下文能力。

在 MoE 架构中,模型通过路由网络为每个输入令牌选择合适的专家模块。对于具有 n 个专家的网络,用于推理的 MoE 模块的输出为:
其中,z=Router(x,r)。在本文中,Router使用线性网络,Gating是门函数(通常是softmax),Expert是FNN层。
MoE通过TopK功能进行专家分配。这个专家路由过程是不可微的,因此在反向传播期间无法获得推导。
对此,传统MoE训练将TopK视为常数,仅使用Gating反向传播并计算路由权重梯度,相当于用门控梯度代替路由梯度。
这有点粗糙。
如果我无法指导怎么办?
正好在这篇文章之前有一个作品(SparseMixer):

论文地址:
受到直通梯度估计器的启发,作者扩展了之前的工作,提出了SparseMixer-v2。
作者首先在模型训练中用离散变量的随机采样代替TopK函数,然后应用Heun的三阶方法来逼近专家路由梯度,并构造改进的反向传播以给出专家路由在数学上合理的梯度估计。

在之前的工作中,SparseMixer的有效性在神经机器翻译任务和ELECTRA语言模型训练中得到了证明。
在GRIN MoE的开发过程中,SparseMixer-v2终于有机会大规模用于自回归语言模型训练。
作者用2.5T token训练了两个16×0.9B MoE。一种遵循 GRIN MoE 中使用的相同方案,另一种用传统的 GShard 方法取代 SparseMixer-v2。
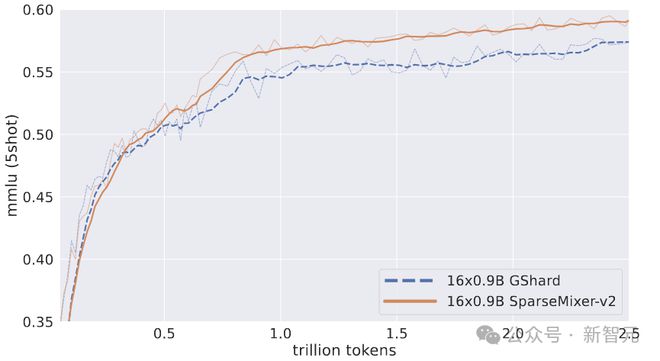
如上图所示,SparseMixer-v2的性能提升扩展到16×0.9B规模的自回归语言模型训练。
GShard 在前 0.5T 令牌上表现更好,但 SparseMixer-v2 在训练的后期阶段取得了更强的性能。
专家模型不需要专家并行性
传统的 MoE 训练使用专家并行性。简单的理解就是给不同的显卡分配不同的专家。
一个明显的问题是负载不平衡。有些专家会被分配更多的代币,而有些专家则非常闲置。

之前的方法是设定一个阈值,比如1000个代币分配给4个专家,每人应该是250个,此时每张卡最多只能算250个代币,如果超过就会被丢弃直接(发送到下一级)。
在这篇文章中,作者使用数据并行、管道并行和张量并行来训练GRIN MoE。
此外,对于没有专家并行性的 MoE 计算,作者发现 Megablocks 包非常有用,其 grouped_GEMM 内核和包装器的性能更好。
应用这些新的工程方法可以避免专家并行并消除丢弃令牌的需要。
最终,与具有相同激活参数的密集模型相比,我们的方法实现了训练效率超过 80% 的提升。
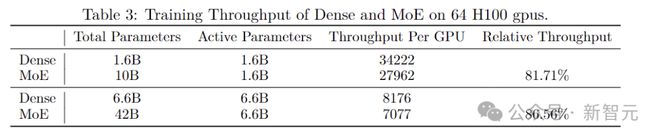
在上表中,作者将两个不同大小的 MoE 模型与具有相同数量激活参数的密集模型进行了比较,并使用相同的硬件测量了它们的训练吞吐量。
尽管MoE的参数总数是稠密模型的六倍多,但在实验中实现了超过80%的相对吞吐量,证实使用GRIN MoE方法的模型具有显着的计算扩展潜力。
(PS:密集模型的吞吐量是在与MoE模型相同的并行度设置下测量的,这里的比较是为了研究密集激活网络(非MoE)和稀疏激活网络(MoE)的GPU内核效率)
此外,当扩大模型尺寸时,密集模型和 MoE 模型表现出类似的减速模式,因此 6.6B 密集模型的训练吞吐量比 1.6B 密集模型慢约 4.19 倍(后者的训练吞吐量低 4 倍)参数) )。同样,42B MoE 模型的训练吞吐量比 10B MoE 模型慢约 3.96 倍(对应参数少 4.2 倍)。
平行实验
仅使用管道并行性,通过进一步划分 GPU 之间的不同层,可以将专家的最大数量从 16 扩展到 32。然而,如果进一步增加专家数量,单层参数就会过多,GPU 无法容纳。
所以下一维采用张量并行。
专家并行在前向和后向计算中具有两个 all-to-all 通信开销,而张量并行在前向和后向计算中具有两个 all-reduce 通信开销。
相比之下,all-reduce 操作的延迟较高,但可以通过仔细安排正向和反向计算来重叠部分开销。
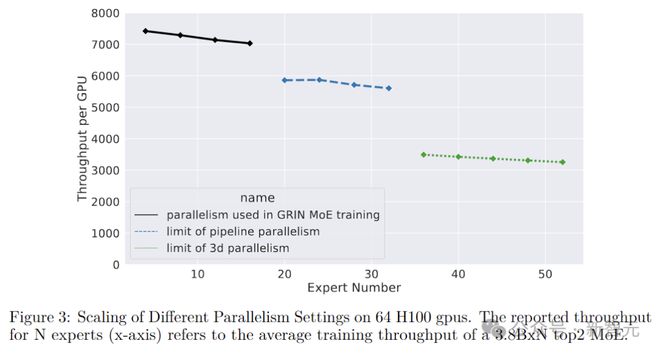
如上图所示,通过管道并行和张量并行相结合,系统支持的最大专家数量扩展至52个(共132B个参数)。
这个数字是因为实验只使用了 64 个 GPU,而模型最多可以分为 64 个阶段。如果GPU更多,还可以继续向上扩展。
然而,作者还指出,使用更复杂的并行性通常会导致计算吞吐量降低。
负载平衡
正如前面提到的,本文没有使用专家并行,但负载不平衡的事实仍然存在。
作者这里通过调整负载均衡损失来调整全局负载均衡。常见的负载平衡损耗定义为:
其中,α为超参数,n为专家数量,fi为分配给专家的代币比例。
传统方法在不同的 GPU 上本地计算 fi,因此负载平衡惩罚将调节本地专家负载平衡并减轻令牌丢弃。
在这篇文章中,作者通过计算全局fi(比如数据并行过程中组内的all-reduce)来修改负载均衡损失,并调整专家负载来实现全局均衡。
虽然这种调整会带来额外的通信开销,类似于张量并行,但这些通信也可以与计算重叠,从而在很大程度上减少额外的延迟。
最后我们放一个测试结果来展示GRIN MoE的数学推理能力:
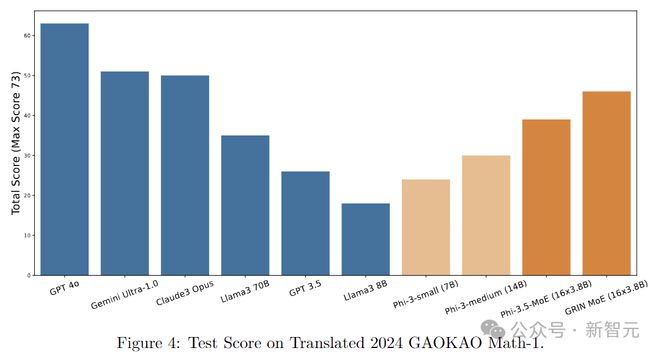
作者注:我们对新发布的高考(中国一年一度的全国本科入学考试)数学试题进行了案例研究。该考试以其严格的安全协议而闻名,是评估人工智能模型回答数学问题的能力的理想测试场。请注意,GRIN 教育部的培训将于太平洋标准时间 6 月 3 日结束,2024 年高考将于中国标准时间 6 月 7 日开始。
参考:

