扩散模型其实就是生物学的进化算法!
这一结论来自“新常春藤”塔夫茨大学最近发表的一项研究:

论文地址:
论文的最终老板是迈克尔·莱文(Michael Levin),美国发育和合成生物学家,毕业于哈佛大学,获得博士学位。目前担任塔夫茨大学艾伦探索中心主任。
迈克尔·莱文长期从事生物电、人工生命等诸多生物学相关课题的研究。他在 NeurIPS 2018 上做了题为“What Bodies Think about: Bioelectric Computation Outside the Nervous System”的精彩演讲:

视频地址:
在 ALife 2020 上,Michael Levin 还阐述了“机器人癌症”的话题:“胚胎发生和再生的生物电可以教会我们关于非常规计算、认知和生命软件的知识。”
这位精通计算机的生物学专家如何理解“扩散模型是进化算法”?
答案是数学。
扩散模型的本质
在生物圈中,至少有两个过程可以概括和创造新事物:
进化:生物体通过自然选择适应环境的缓慢过程(需要多代);学习:个体有机体获取知识和概括主观经验(自己的一代)的快速过程。
研究人员不断探索进化与学习之间的联系,从 Hinton 的经典著作《学习如何引导进化》(1987 年)到 Vanchurin、Wolf、Katsnelson 和 Koonin 的《走向作为多层次学习的进化理论》(2022-2023),以及沃森和莱文的《进化和发展的集体智慧》(2023)。

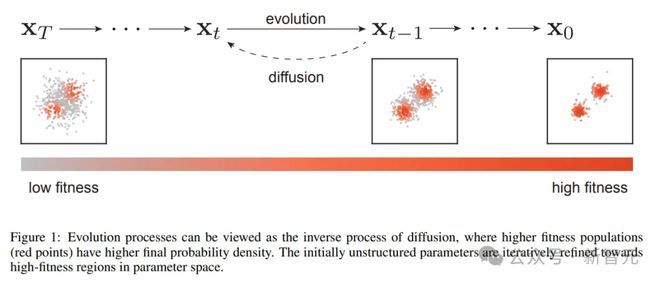
目前的工作认为,在扩散模型的框架中,生成模型执行顺序随机去噪,这可以通过执行自然选择、突变和生殖隔离的进化过程来理解。
前向扩散过程将图像作为输入(可以是任何其他信号)并逐渐按顺序添加噪声,直到它变成一团乱七八糟的噪声。
相比之下,扩散模型的逆过程是一个去噪过程,以噪声为输入,依次去除噪声,最终发现隐藏在噪声背后的图像。

原始扩散模型:
想象一个复杂的任务(例如,找到飞机机翼的最佳形状),我们可以从创建一组随机解决方案开始 - 就像自然界中的一群生物一样。然后根据特定标准(例如飞行条件)评估每个解决方案。
在此过程中,不同解决方案的优点可以“交叉”(从一个解决方案中获取一些参数,从另一个解决方案中获取其他参数),有时可以随机更改这些解决方案(的参数)以获得新版本的解决方案。计划。
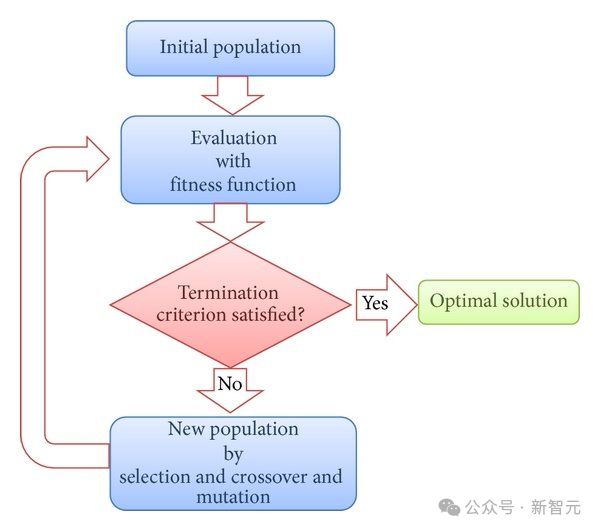
多次重复这个过程,就像自然选择一样,通过遗传和突变,更成功的版本得以生存并继续发展。
通常,参数空间的结构是先验未知的,因此初始总体通常以标准正态分布开始。这种方法的主要优点是它不需要精确了解任务的工作原理 - 只需能够评估解决方案的质量就足够了。
扩散模型直接根据每个时间步的样本噪声来预测原始数据样本:
样本x的估计可以表示为条件概率,可以结合贝叶斯公式得到:
基于深度学习的扩散模型使用均方误差损失进行训练,因此估计函数变为:
高斯项仅对局部邻居敏感。简化上面的公式:
由此可见,扩散模型和进化算法都涉及迭代数据更新和从复杂分布中采样新对象,并且都是定向更新和随机扰动的组合。
在进化的情况下,是选择+变异,在扩散的情况下,是随机噪声+学习去噪。
这就提出了一个问题:这两个过程的机制是否从根本上相互关联?生物进化和生成模型之间是否存在深刻的数学二元性?
扩散与进化
首先,作者从生成模型的角度分析了进化论。
观察生物圈中的物种种群,变异的进化过程可以理解为基因型和表型分布的变化。突变和选择共同改变了这些分布的形状。
许多受生物学启发的进化算法通过维护和迭代大量群体的分布来优化目标函数。
相同的概念(分布变换)是许多生成模型的核心:VAE、GAN 和扩散模型学习将简单分布(例如标准高斯分布)变换为更复杂的分布(分布中的样本表示有意义的图像、声音)等)和文本)。
另一方面,扩散也可以从进化的角度来看待。
在训练过程中,干扰逐渐添加到数据点中,模型学习预测这种干扰以逆转该过程。在采样阶段,模型从高斯分布开始,通过降噪逐渐更新数据点。
在这种情况下,定向降噪可以理解为定向选择,每一步都添加类似于突变的小噪声,与生物体的进化过程一致。
而如果进化过程逆转,那些高度适应自然的进化种群就会逐渐消解,类似于正向扩散过程。
考虑到统计物理学中的能量和概率,可以通过将适应度映射到概率密度(高适应度对应于高概率密度)来将进化任务与生成任务联系起来。

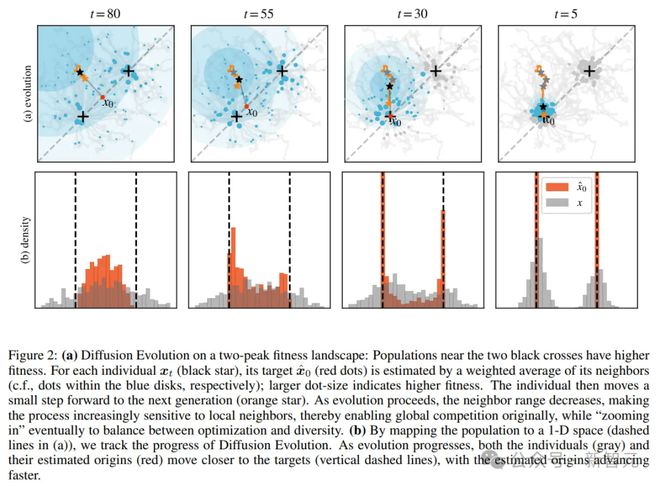
作者最终在数学上推导了一种名为 Diffusion Evolution 的新算法,该算法基于迭代误差修正进行优化,与扩散模型类似,但不依赖于神经网络:
1)从一组随机解决方案开始(如扩散模型中的噪声); 2)在每一步,每个解都通过适应度函数进行评估,并且每个解都被“去噪”(类似于通过邻居解的加权平均值估计),并向前迈出一小步,同时添加一个小的随机突变; 3)逐渐减小邻居搜索半径(先全局探索解空间,再局部优化)
与许多通常收敛于单个解决方案的经典进化算法不同,扩散进化可以同时发现并维护多个性能良好的解决方案。
实验
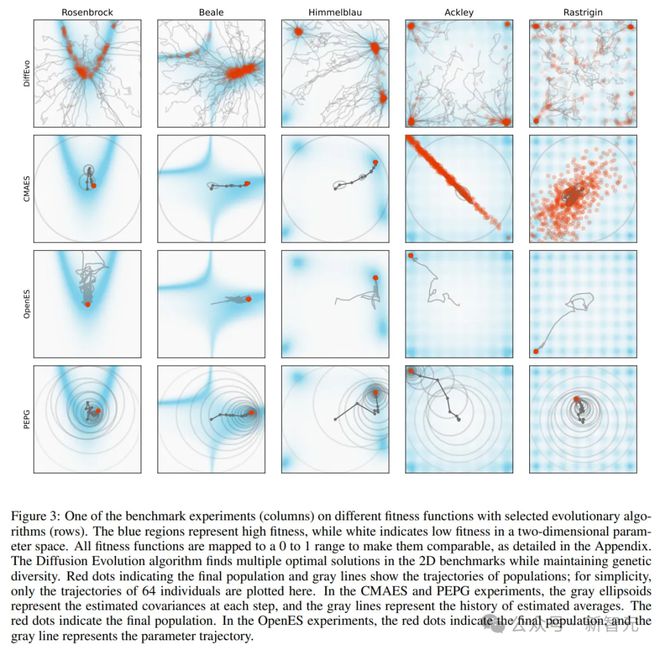
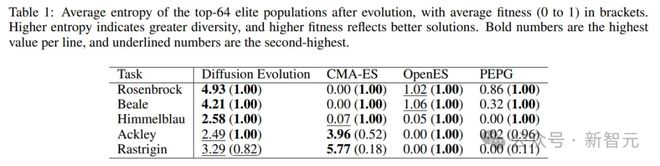
研究人员在多个 2D 优化场景(Rosenbrock 和 Beale 的一个最优值,Himmelblau、Ackley 和 Rastrigin 的多个最优值)中进行了实验,并与其他进化算法(CMA-ES、OpenES 和 PEPG)进行了比较。
每种方法运行进化算法 100 次,每次实验的群体大小为 512,使用 25 次迭代(OpenES 需要 1000 步才能收敛)。
结果表明,扩散进化找到了高质量且多样化的解决方案,特别是在最后三种情况下,其他方法遇到困难并且倾向于收敛到单一解决方案。
在进化算法中,适应度评估通常是计算成本最高的操作,作者通过借用扩散模型工作中的余弦调度来减少迭代次数。
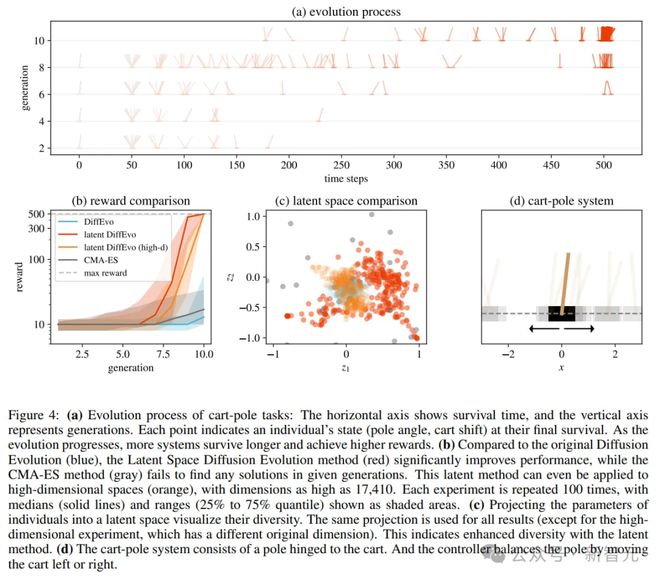
在另一个实验中,研究人员受到潜在空间扩散模型(通过探索低维潜在空间来解决高维参数空间问题)的启发,提出了潜在空间扩散进化(Latent Space Diffusion Evolution)。
学习和进化本质上是做同样的事情。沿着这条路,我们可以继续思考:
模型推理是有限的,但真正的进化可能是无限的、开放式的。如何使扩散进化适应开放环境?
其他版本的扩散模型会带来新的进化算法吗?扩散模型中的归纳偏差可以引入进化算法吗?扩散模型可以用进化思想来改进吗?
参考:

