算力需求相较于 AdamW 直接下降了 48%,OpenAI 的技术人员所提出的训练优化算法 Muon,被月之暗面团队进一步推进了。
团队发现了 Muon 方法的 Scaling Law 这一情况。团队对其进行了改进,并且证明了 Muon 对于更大的模型也是同样适用的。
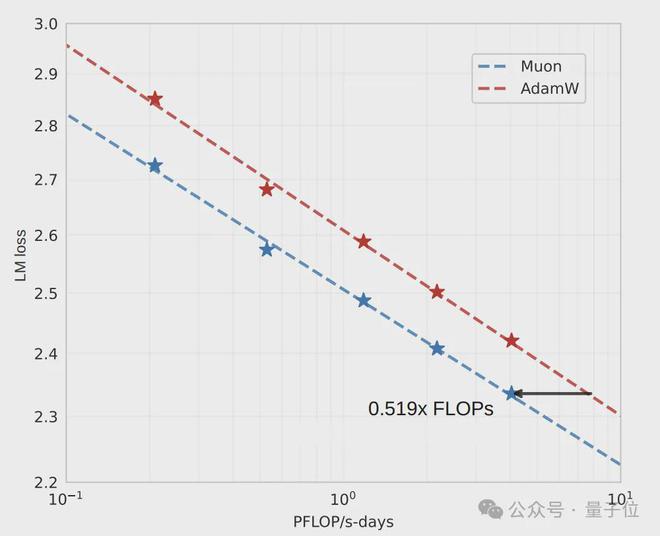
不同的 Llama 架构模型参数量最高可达 1.5B,在这些模型上,改进后的 Muon 的算力需求只是 AdamW 的 52%。
团队训练出了一个 16B 的 MoE 模型,这个模型是基于 DeepSeek 架构的,并且团队将其与改进后的优化算法一同开源了。
Muon 技术博客发布时主要是适用于规模较小的模型以及数据集的。作者留下了以下三个悬而未决的问题:
消息一经发出,当时 Muon 的那些作者们都感到十分激动。其中主要作者 Keller Jordan 称,这是 Muon 实现规模化的首个成功报告,并且为团队送上了祝贺。
另一名贡献者,当时在负责 Muon 规模化实验的 Hyperbolic Labs 担任联合创始人兼首席技术官的 Yuchen Jin 也表明,月暗团队的这一成果,属于 Muon 的一次胜利。

将AdamW特点引入Muon
在开始介绍月暗团队的工作之前,首先要了解一下 Muon 是何种技术。
这是一种用于神经网络隐藏层的优化器,其参数是 2D 的。它的主要作者是 Keller Jordan,来自 OpenAI 深度学习团队。
这项成果是在去年 12 月 8 日发表的。Keller 是在去年 12 月加入 OpenAI 的。
Muon 的核心思想在于通过正交化梯度来更新矩阵。这样做可以避免参数更新陷入局部极小值的情况。从而使模型能够学习到更为多样化的特征表示。
Muon在 94%的精度下,将 CIFAR - 10 在 A100 上的训练时间从 3.3 秒缩短到了 2.6 秒。

当时 Muon 团队仅证明了其在小型模型和数据集上是可行的。然而,对于较大的模型是否能够适用,这是一个未知的情况。
现在经过月暗团队的改进,Muon被证明对于更大的模型是适用的,并且对于更大的数据集也是适用的。
团队针对模型本身,吸收了 AdamW 中的一些特点,并将其移植到了 Muon 当中,具体包含两个方面。
引入了权重衰减机制,在权重更新公式里添加了一项,该项带有衰减系数。
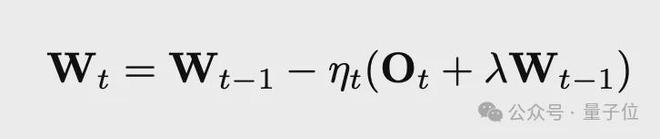
作者发现直接将 Muon 应用到大规模训练时,会出现模型权重和层输出的幅度持续增长的情况,这种情况最终会超出 bf16 的高精度表示范围,从而损害模型性能,这就是这样做的原因。
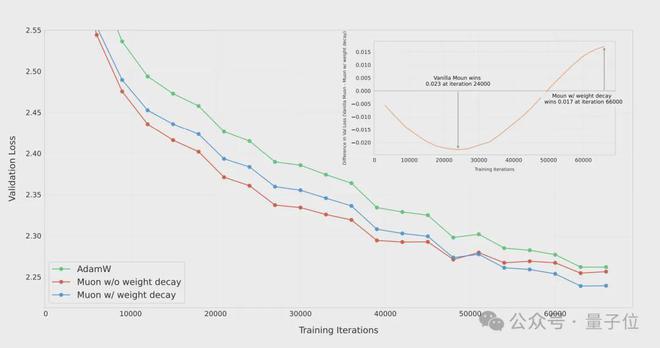
在训练一个 8 亿参数模型达到 100B tokens 时(这个量约为 5 倍计算预算的最优值),团队对 AdamW、没有权重衰减的 Muon 以及带有权重衰减的 Muon 进行了对比。
结果表明,在过拟合阶段,带权重衰减的 Muon 取得了最好的效果,这验证了权重衰减是有必要的。
第二项改进在于对 Muon 的参数更新尺度进行了调整。这样做使得不同形状矩阵的参数更新幅度能够保持一致,同时也能与 AdamW 的更新幅度相匹配。
Muon 有一个特点,即对于矩阵参数,若其形状为[A,B],那么它的理论更新幅度是 sqrt(1/max(A,B))。
这使得不同形状矩阵参数的更新幅度存在很大差异。例如,对于 MLP 这种宽矩阵而言,其更新幅度会过小;而当把每个 head 看作独立矩阵时,更新幅度又会过大。
这个幅度和 AdamW 不一致,并且给超参数的设置带来了困难。
作者为了使不同矩阵参数的更新幅度能够相匹配,并且与 AdamW 保持一致,尝试了若干种改进方案,最终决定直接依据形状来对每个参数的学习率进行调整。
0.2 是一个通过实验确定的常数,它的作用是将 Muon 的更新尺度与 AdamW 进行对齐。

要将 Muon 用于更大规模的训练,除了对 Muon 本身进行改进之外,还需要把它扩展到分布式训练环境中。
Muon 计算正交化的更新量需要完整的梯度矩阵。现有的分布式训练框架,像 ZeRO-1、Megatron-LM 等,都假设优化器状态可以独立地按元素切分到不同设备上。因此,这些框架无法直接支持 Muon。
论文作者为了解决这个问题,提出了分布式 Muon 的并行化策略。
它在ZeRO-1的基础上引入了两个额外的操作:
这种实现方式在将内存占用和通信开销最小化的同时,把原始 Muon 算法的数学性质最大限度地保留了下来。

证明Muon扩展可行性
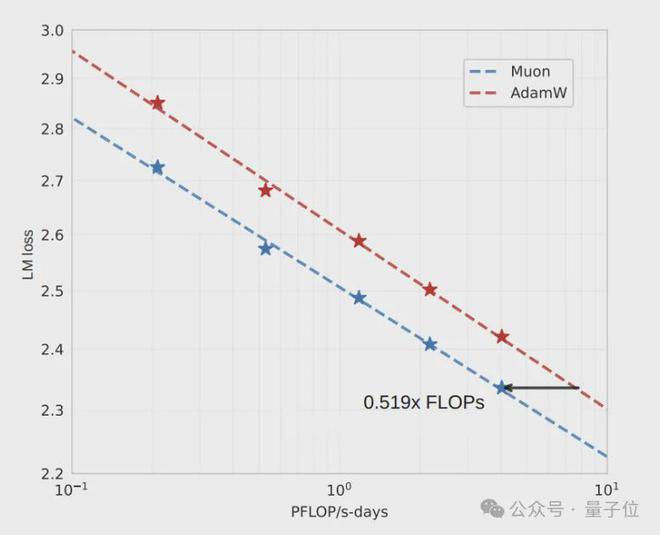
作者基于上述的 Muon 进行了改进,从而取得了以下成果。作者针对 Llama 架构的一系列稠密模型,开展了 Muon 与 AdamW 的模型缩放对比实验。
结果表明,在计算预算处于最优状态时,Muon 的样本效率比 AdamW 高 1.92 倍。这意味着,要达到相当的性能,训练所需的 FLOPS 仅为 AdamW 的 52%。
这一发现证实了Muon在大规模训练中的效率优势
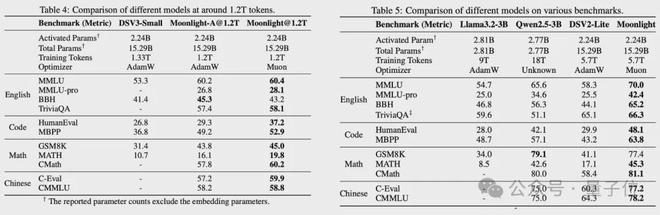
作者以 DeepSeek-V3-Small 架构为基础,然后用改进的 Muon 对 Moonlight 模型进行了训练。
Moonlight 是一个 MoE 模型,它的总参数为 15.29B,激活参数为 2.24B,训练的 token 量是 5.7T。
Moonlight 在各类任务上取得了明显更好的性能。其中包括与相同规模和数据量的模型相比,在英语理解与推理方面,如 MMLU、TriviaQA、BBH 等任务;在代码生成方面,如 Humaneval、MBPP 等任务;在数学推理方面,如 GSM8K、MATH、CMATH 等任务;以及在中文理解方面,如 C-eval、CMMLU 等任务。
Moonlight 展现出了极强的竞争力,即便与那些使用更大数据集来进行训练的稠密模型相比较。
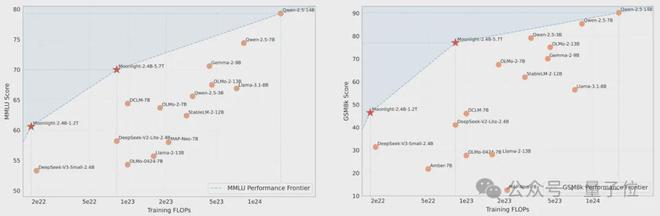
对比多个知名语言模型后发现,Moonlight 在性能与训练预算所构成的平面上推动了帕累托前沿。
帕累托前沿是经济学和管理学中的一个概念,它描述的是多目标决策问题中所有可能的最优解的集合。这些解在多个目标之间取得了最佳平衡。在帕累托前沿上的每一个点,都意味着一个目标的改善必然会以牺牲另一个目标为代价。所以,它代表了在多个目标之间实现的最佳权衡。
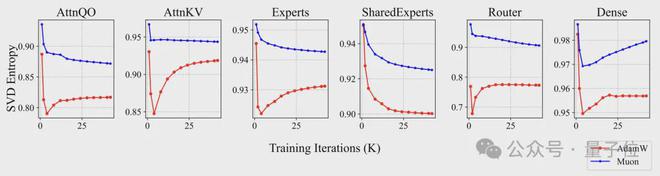
作者为了进一步剖析 Muon 更新矩阵参数的内在机理,将 Muon 和 AdamW 训练所得模型在不同训练阶段的参数矩阵奇异值谱进行了对比。
结果表明,在各层各类参数上,Muon 优化的矩阵的奇异值熵总是比 AdamW 的高。这从经验层面验证了 Muon 通过正交化去学习更具多样性表示的这种直觉。
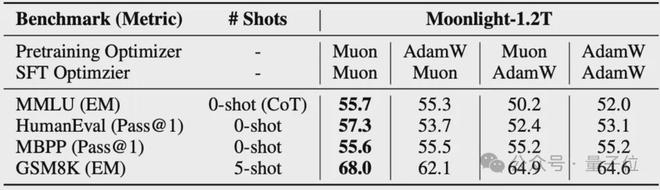
作者首先在 Moonlight 模型的基础上进行了探索。接着,探索了 Muon 在指导微调阶段的效果。最后,结果显示,在预训练和微调阶段都使用 Muon 的效果最为出色。
技术报告:
Code:
Moonlight模型:

