要是存在这样一个人,他写下了如此复杂的公式,还宣称这是受到女神在梦中给予的启发才得到的,那么大家伙儿一般会送给他两个字:民科。
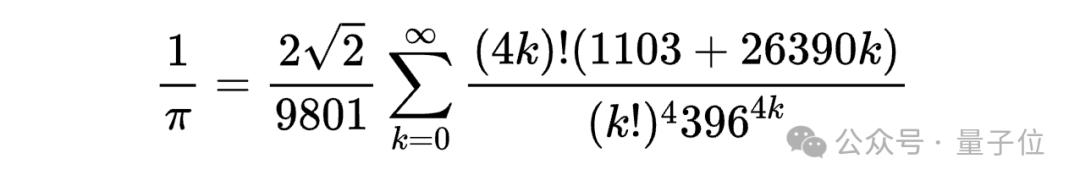
但这个人一生中写下数千次类似的数学公式和命题,在此后的100年间,这些公式和命题不断地被证实是正确的,那么就只有一个可能——
他是拉马努金。

它再度火爆,原因在于直至今日,数学界持续出现最新发现,这些发现用于验证他当年留下的“谜题” 。
拉马努金,是一位在全数学界都被公认为神人的人物,他被视作数学史上最伟大的天才之一 。
他没有接受过正统数学教育,在印度挂科,连本科学位都没拿到,却凭借惊人的数学直觉征服了数学大师G.H.哈代,剑桥大学三一学院因此破例向他打开大门 。
他32岁就英年早逝,他从事数学职业的时间只有短短6年,然而他的数学笔记至今仍是传奇,笔记中留下了近4000个公式,其中很多公式在后来都被证明是正确的。
他的恩师哈代甚至以开玩笑的方式表示,自己对于数学所做出的最大贡献便是发现了拉马努金。
和拉马努金的交往是我一生中唯一的浪漫事件。

直到今天,后辈数学家们仍在追赶着拉马努金的步伐。
2024年9月,弗吉尼亚大学的数学家小野肯(Ken Ono)和他的合作者们,在PNAS(美国国家科学院院刊)上发表了一篇论文,该论文是关于罗杰斯 - 拉马努金恒等式的应用,他们把这个恒等式用于检测质数。

“梦中女神的启示”
拉马努金传奇故事的构成要素之一,是他独特的做数学的方式。
简单来说就是三个字:凭直觉。
毕竟按照常规思维去评判,你会发现很难理解一位20世纪10年代的数学家,他是如何写出那么多表达式的,而那些表达式看上去似乎只有计算机才能完成 。
他写给哈代的第一封信,使哈代发出“我从未见过像这样的东西”的惊呼,信里的数学结果呈现出这样的情况:
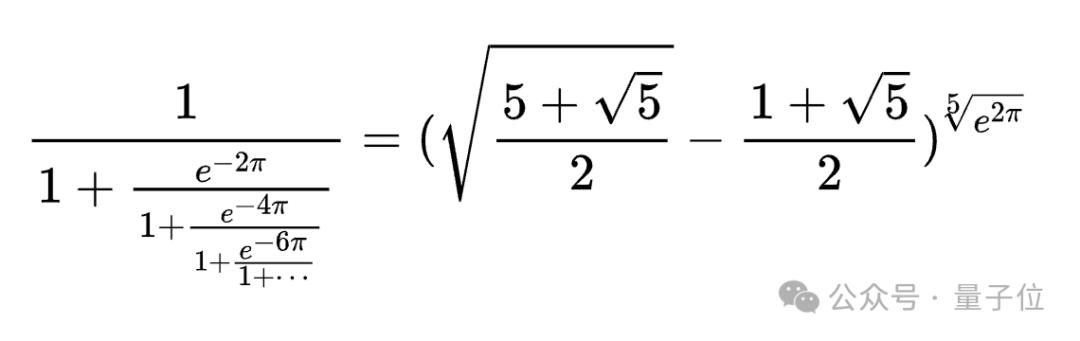
拉马努金自己常宣称,他的直觉与灵感源于女神托梦,他是婆罗门教徒,在梦中获得灵感,醒来后便将这些表达式记在笔记中 。
在如今,拉马努金影响极为深远的研究涵盖了罗杰斯 - 拉马努金恒等式。
这是与基本超几何级数和整数拆分相关的两个恒等式。
第一个恒等式是:
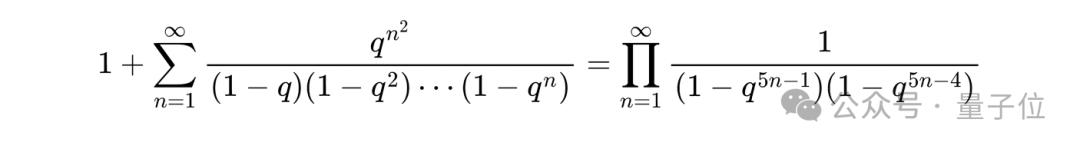
第二个恒等式是:
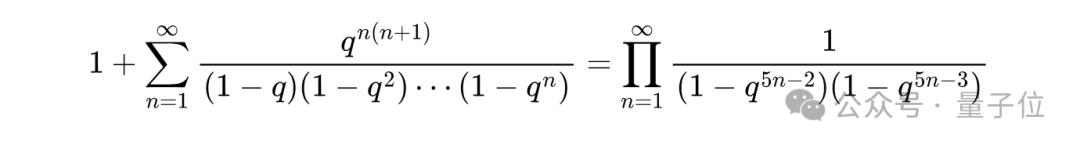
后世数学家们发现,罗杰斯 - 拉马努金恒等式与其他数学领域存在深切关联,这些领域比如有统计物理学和表示论 。
20世纪80年代,罗格斯大学数学家James Lepowsky和Robert Wilson运用顶点算子代数理论,给罗杰斯-拉马努金恒等式提供了一个新的表示论证明。
顶点算子代数理论在弦论发展进程里起到了重要作用,它在群论最大成果之一即怪兽月光理论的证明当中发挥了关键作用。
拉马努金猜想,是数论研究里的一个重要里程碑,也是模形式研究中的一个重要里程碑。现代数学研究中最大的单项项目是朗兰兹纲领,它和拉马努金猜想有着紧密的联系。
拉马努金猜想一般是针对模形式的τ函数系数大小所提出的猜想 ,该猜想由拉马努金提出 ,具体内容为对于:
其中,对于素数p,τ(p)的绝对值不会超过
简单来讲,就是这个数列里的数字,虽然会增大,但是不会增大得太快,也不会增大得太大。
1973年,皮埃尔·德利涅(Pierre Deligne)证明了这个猜想。
朗兰兹纲领的核心是函子性猜想,该猜想描述了不同代数群的自守表示之间存在深刻联系,函子性猜想包含诸多著名猜想,拉马努金猜想是其中之一 。
自学成才的数学鬼才
这位数学家受到了女神的眷顾,在如今的数学史上,他已成为一个无法避开的名字,一个闪耀着光芒的名字 。
但在1887年他出生时,他的父母或许怎么也想不到,他们身处这样一个没落的印度婆罗门家庭,日后竟会成长出一位传奇的数学鬼才 。
拉马努金出生在印度泰米尔纳德邦埃罗德县,他的父亲是一名小职员,收入微薄,母亲是家庭主妇 。
拉马努金年幼时很快展现出天赋,在小学取得优异学业成绩,他10岁进入中学后才算真正接触到正规数学。

在这样的环境里,事实上,从开始接触数学,到最终发展出属于自己的数学研究成果,拉马努金主要依靠的是自学。
一开始,他跟着家里的两个大学生租户学习数学知识,到了11岁,两位大学生没什么能再教他的了,于是,他们借给拉马努金一本高等三角学的书,让他继续自学。
拉马努金13岁的时候,把这本书彻底钻研明白了,甚至还凭借自身能力发现了一些复杂的定理 。
他以全区最好成绩升入当地高中,之后,凭借个人直觉,凭借逻辑思维,他独立推导了《纯粹及应用数学的基本成果概要》中的大量数学公式。
具体来讲,他认真研究了书中的5000个数学定理,之后发现了伯努利数,并且以具有里程碑意义的方式,把欧拉 - 马斯切罗尼常数计算到了小数点后15位。
到高中毕业的时候,他获得了K. Ranganatha Rao数学奖,校长称赞他的成绩远超满分水平。
只可惜,拉马努金对数学的过度专注让他在大学时期遭遇了挫折。
这一阶段的求学经历十分混乱,期间经历了换校,学位考试两度失败,数学只答自己感兴趣的,其他科目成绩不佳,最终肄业,没有拿到学位证。
他大学失败后,心情沮丧,于是选择离家出走,结果母亲在报上登了一份寻人启事 。

之后他一直陷于生活窘迫之中,不过仍未放弃独立数学研究。
直到23岁那年,他认识了税务部门公务员V. Ramaswamy Aiyer,这个人创立了印度数学会,那时他已结束数学会第一任秘书职务 。
命运的齿轮就此转动。
最开始的时候,无业的拉马努金一心只想进入税务部门工作,所以他向Aiyer展示了自己的数学笔记本。
看完笔记后,Aiyer立刻深切地感觉到,不能让拉马努金的才华在税务底层部门被埋没,于是他写了一封介绍信,把拉马努金推荐给了自己的数学家朋友们。
这群人对他极为看好,经过层层举荐,拉马努金来到了印度数学会秘书R. Ramachandra Rao面前。
这位秘书对他的研究印象颇为深刻,不过考虑到拉马努金的知识背景,便对他作者身份的真实性产生了怀疑。
经过多方努力,最终拉马努金拿到了一次面谈机会:
在这位秘书跟前,他滔滔不绝地谈论椭圆积分,谈论超几何级数,谈论发散级数理论……
当得知拉马努金迫切需要工作和财政支持后,这位秘书把他推荐到了一所大学担任研究员,为他的研究提供经济资助,最终征服了对方。
后来,拉马努金的研究成果发表在《印度数学会杂志》上。
这中间还发生了一件有意思的事:
当时,他把一个方程投稿给期刊,这个方程是无限嵌套根式的,是以谜题的形式投稿的,他想看看能收到哪些回答。
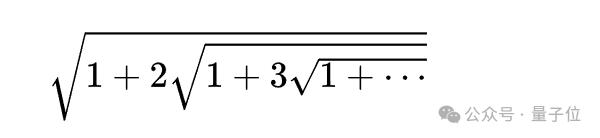
结果等了3个月,没有任何人理他。
拉马努金没有别的办法,只能亲自上场,一番快速操作之后,最后在第一本笔记的第105页,写下了无限嵌套根式方程的解决办法。(堪称自己挖坑自己填的第一人)
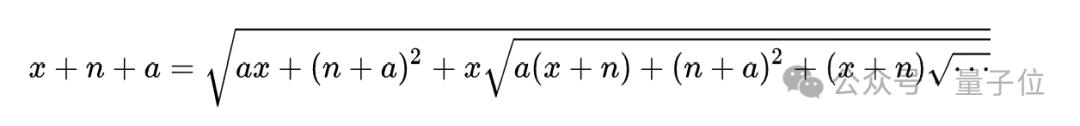
总之在这一时期,拉马努金有工作,同时还利用业余时间搞数学研究,他的生活还算比较平稳。
再往后,为了能让一些工作成果得到更广泛的传播,拉马努金着手给几位英国数学家写信:
我是一名工作人员,我没有接受过大学教育,不过我正在为自己开创一条全新的道路。
信中还有几页是关于数学推演的,其中一部分内容,之前有人进行过推导,另外一部分内容,并不完全正确。
最先接到信的是HF Baker教授和EW Hobson教授,他们没有发表任何评论,直接退回了信件。
然而这并没有使拉马努金知难而退,他依旧把信寄给了那个“仿佛命中注定的人”,此人便是数学家哈代 。
哈代最初看这份手稿时,也认为这是欺诈行为,然而,最后有3个陌生的公式引起了他的注意:
我以前从来没见过这些东西,这些东西彻底把我打败了。它们肯定是真的,要是它们不是真的,那就没有人具备想象力去发明它们 。

震惊过后,哈代产生了惜才的想法,于是他邀请拉马努金前往剑桥大学一起进行研究,还提供了剑桥奖学金。
于是从1914年起,两人开始了合作研究,他们与哈代的另一同事李特尔伍德一起合作,这种合作持续了长达5年的时间。
仅就拉马努金与哈代而言,二人的合作并非易事,哈代追求严谨的证明,拉马努金则更相信直觉。
不过期间二人还是发生了不少有趣的小故事:
有一回,拉马努金生病住进了医院。哈代想要帮他排解烦闷,就告知他出租车的编号是1729,还说这是“一个看上去没什么特别意义的数字” 。
这可激起了拉马努金的反驳,“不,这是个非常有趣的数字。”
他做了进一步的解释,他说,在所有能够用两种方式写成两个自然数立方和的数字当中,它是最小的那一个 。
1729=1^3+12^3=9^3+10^3
这个故事后来被用以界定“的士数” ,(不太理解这些数学家的趣味doge)

后来,拉马努金凭借在高度复合数方面的工作,获得了研究型文学学士学位,这是博士学位的前身,并且他当选为伦敦数学会会员。
31岁那年,他当选为英国皇家学会会员,凭借的是“对椭圆函数及对数论的贡献”,他是史上最年轻的该学会会员,他还是该机构认可的第二位印度人。
然而让人意想不到的是,刚刚收获巨大成就的拉马努金,却迅速迈向了故事的结局。
1920年,拉马努金因身体不适返回印度,同年,他32岁便英年早逝。
当时人们认为,拉马努金可能死于结核病,直到1994年,有医生对他的医疗记录和症状进行分析,得出新结论,他死于肝阿米巴病。
理由是,拉马努金在离开印度之前,曾经患过两次痢疾,阿米巴痢疾有可能潜伏数年时间,并且会导致肝阿米巴病 。
后来有医生称,要是当时能获得正确的诊疗,这种病一般是能够被治愈的 。
这也让后人一直感到无比遗憾:
人们专门设立了“拉马努金奖”,以此纪念他,该奖项每年由位于他的故乡贡伯戈讷姆的Shanmugha文理工研究院(SASTRA)颁发,奖金为10000美元。
获奖者需满足两个条件:
在拉马努金研究领域做出杰出贡献的数学家
获奖时年龄需在32岁以下(正好是拉马努金去世时候的年纪)
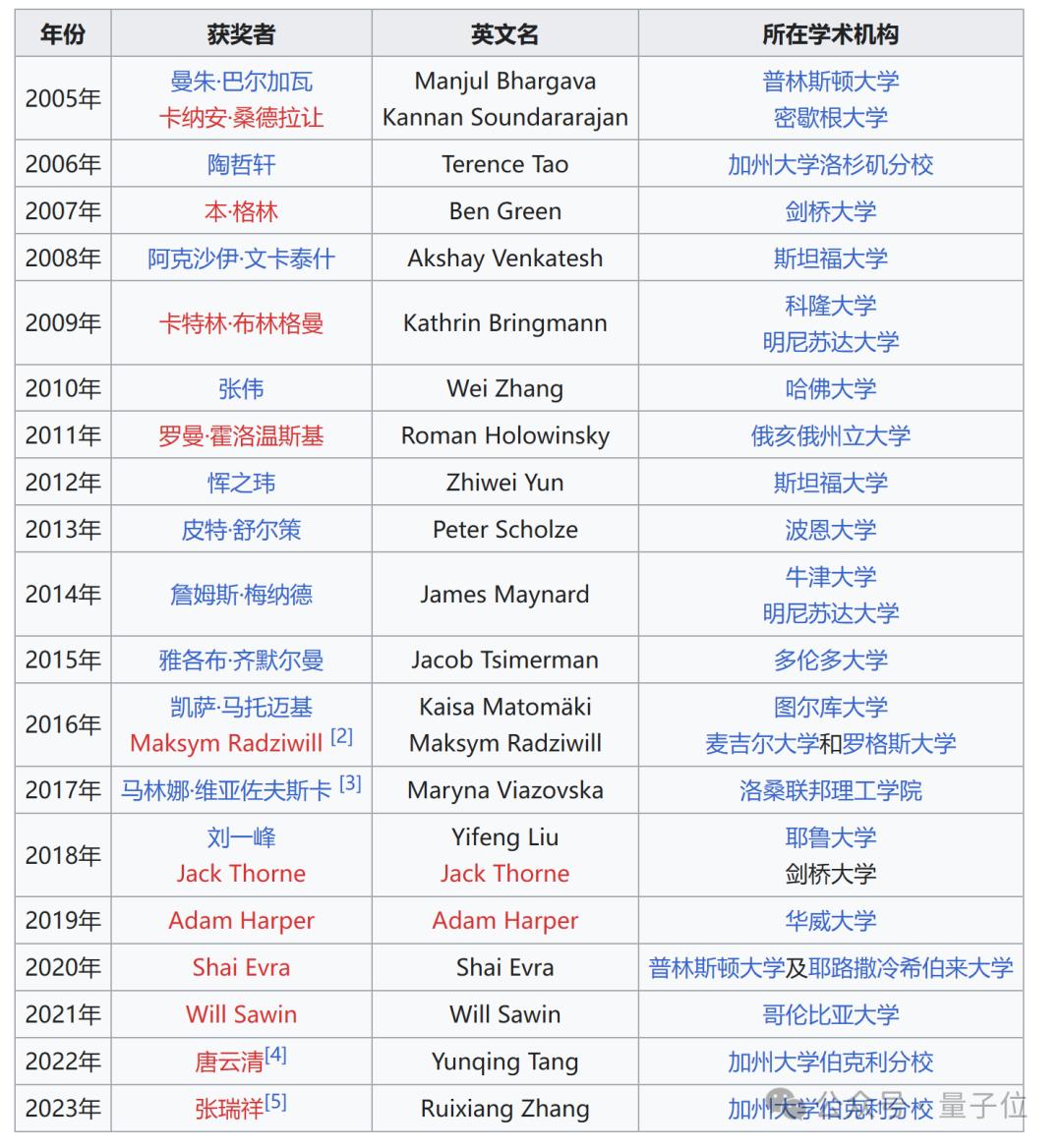
该奖从2005年开始颁发,到现在已经有22位获得者,其中有陶哲轩、詹姆斯·梅纳德等多位菲尔兹奖得主,还有张伟、恽之玮、刘一峰等出身于北大数院的数学家们。
数学家们仍在追赶拉马努金
从1914年到1920年,实际上,拉马努金作为职业数学家工作的时间只有6年,不过,就像前文所讲的那样,他的成果至今仍影响着数学界的后辈们。
1976年,人们在剑桥大学三一学院的图书馆中有所发现,那是拉马努金生命最后一年的“笔记本” 。
这个“笔记本”由138页纸张组成,这些纸张是散乱的,上面记录了600多个数学公式,然而却没有证明的过程,其中包含拉马努金对模拟θ函数的研究,该函数对计算黑洞的熵很有用 。

拉马努金留下了手稿笔记,其中包含这本“遗失的笔记本”,这些手稿笔记里一共有3900余个公式和定理。
拉马努金本人在笔记中并未留下明确思路,然而后辈数学家们依旧觉得,他为重要理论的开端奠定了基础。
直至今日,数学家们依旧在追寻拉马努金留下的遗产,紧跟这位传奇人物的步伐 。
巴黎西岱大学有位数学家叫侯赛因·莫尔塔达(Hussein Mourtada),他是其中之一 。
他从博士阶段就开始研究奇点理论,他发现,有一种方法能够证明奇点的深层基础结构,而这种方法源自拉马努金在一个世纪以前写下的数学陈述。
简单来说,莫尔塔达在研究简单奇点“胖点”的弧空间,他发现弧空间的结构,这种结构可用罗杰斯 - 拉马努金恒等式来描述。

在此基础上,他和他的学生Pooneh Afsharijoo一同进行探索,探索的对象是许多更复杂的奇点及其弧空间。Pooneh Afsharijoo如今在马德里康普顿斯大学担任博士后研究员,他还发现了新的条件,这些条件扩大了拉马努金原始恒等式的范围。
弗吉尼亚大学数学家小野肯,是拉马努金故事片《知者无涯》(The Man Who Knew Infinity)的副制片和顾问,他更是认为,自己的职业生涯在一定程度上得益于拉马努金的洞察。
2014年,小野与Michael J. Griffin、S. Ole Warnaar共同发表论文,该论文为罗杰斯 - 拉马努金恒等式及其算术性质提供了一个框架,还解决了一个源于拉马努金工作的长期谜团。
2024年9月,他与William Craig以及Jan-Willem van Ittterum一道,运用整数拆分方法检测素数,这一方法同样基于拉马努金的工作,论文已发表在PNAS上。

