发布信息
登陆/注册

软件行业资讯 

当前位置： 首页 软件行业资讯 正文

软件无线电系列——过渡带混叠时的采样定理和正交低通采样

作者：本站编辑      2024-01-27 04:33:13     39

本节目录

一、过渡带混叠时的采样定理1、滤波器的过渡带混叠情况2、过渡带允许混叠时的带通采样定理二、正交低通采样1、正交低通采样原理2、正交低通采样原理的优点

本节内容

一、过渡带混叠时的采样定理

1、滤波器的过渡带混叠情况

对于采样定理来说，无论是Nyquist低通采样还是带通采样定理，采样速率fs都必须大于处理带宽B的两倍，也就是fs≥2B。当然，这里的带宽B指的是ADC采样前的抗混叠滤波器的带宽，也是理想的矩形滤波器。但是，实际工程中，通常是矩形系数为r的梯形滤波器，其中r=Br/B。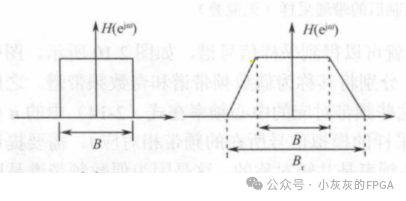

上图中左边为理想的矩形滤波器，右边是矩形系数为r的梯形滤波器。实际上软件无线电所需要处理的带宽是B,滤波器非理想所造成的滤波器实际带宽为Br。如果不考虑滤波器过渡带中的信号可以混叠，那么根据Nyquist采样定理，此时的采样速率fs必须满足fs≥2Br。当然这样会导致采样速率的增加。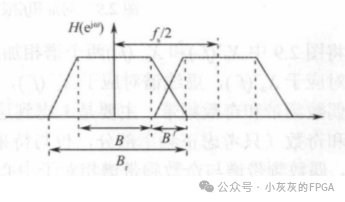
何为滤波器的过渡带混叠情况？

在设计抗混叠滤波器的时候，一般是不允许在过渡带内存在有用信号的，但这里指的是有用信号，其实可以存在一些不需要处理的信号，因此过渡带部分实际上是允许混叠的。也就是上图中B'带宽内的信号，不存在用于软件无线电数据处理的信号。根据矩形系数r，滤波器的过渡带B'的表达式为：
B'=((r-1)/2)×B
从上图中可知，若要满足通带B内的信号不会发生混叠,此时的fs必须满足：
fs/2≥B+B'fs≥2×(B+((r-1)/2)×B)fs≥(r+1)×B

二、过渡带允许混叠时的带通采样定理

在任何一个中心频率为f0，带宽为B的某一带通信号x(t)，如果同时满足以下条件：f0=((2n+1)/4)×fs且fs≥(r+1)×B，其中，n=0,1,2……，n为正整数，r指的是抗混叠滤波器的矩形系数，原始信号x(t)可用其采样信号x(n)=x(nTs)来表示，其中Ts=1/fs，fs为采样频率。
过渡带允许混叠时的带通采样定理，不仅有效降低了采样速率，同时在采样公式中引入矩形系数r，使得在实际工程应用中，有了两个可供调整的参数，一个是带通信号的中心频率f0，另一个是滤波器矩形系数r,增加的工程设计的灵活性。
将考虑过渡带允许混叠时的采样率与不考虑混叠时的采样率比较，降低的倍数为：
g=2Br/((r+1)B)
g=2r/(r+1)
从上式中可以得出，抗混叠滤波器的矩形系数越差，也就是r值越大，此时降低的倍数也越大。以一个实际矢量考虑，当抗混叠滤波器的矩形系数r为3时，此时的降低倍数g=1.5,也就是不考虑混叠时的采样速率是考虑混叠时的采样速率的1.5倍，假设系统中带宽B=50MHz,那么不考虑混叠时的采样速率为2×Br=2×r×B=300MHz,考虑混叠时的采样速率为(r+1)×B=200MHz，满足上述的比例1.5。

二、正交低通采样

1、正交低通采样原理

通常软件无线电所覆盖的频率范围一般要求都比较宽，比如从0.1MHz到5GHz，甚至现在的6G，只有宽的频带才具有广泛的适应性。当然，这样带来了问题，如果根据Nyquist低通采样定理，6G需要的采样速率至少大于12GHz。因此软件无线电中的低通采样一般采用正交混频的办法来实现，也就是通过一个正交混频器先把射频信号混频到相互正交的两个基带上再进行低通采样。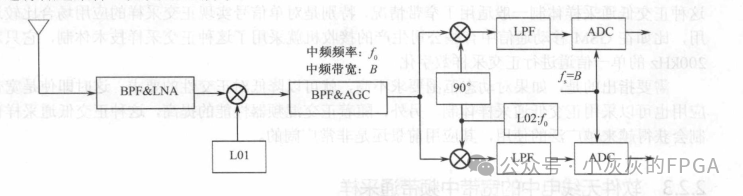

正交低通采样的基本原理：首先通过第一个混频器把某一频带的射频信号变换为合适的宽度中频信号，然后由正交的两个第二混频器把该中频信号变换为两个正交的基带信号I(t)、Q(t)，即零中频信号。这两个正交信号是零中频的低通型的，经过低通滤波后送到ADC进行低通采样。

2、正交低通采样原理的优点

这样做得好处是什么？
由于这两个正交信号是零中频的低通信号，采样的频率只需要大于中频带宽即可，而不需要两倍的中频带宽。经过第一混频器混频后的中频带通信号，中频频率为f0,通过一个复本振e^(-jω0t)将该中频信号的正频谱部分搬移到零中频，即进行运算：
xB(t)=x(t)×e^(-jω0t)=x(t)×cos(ω0t)-j×x(t)×sin(ω0t)
对该信号进行低通滤波滤除x(t)的高频部分,经过搬移中心频率已经是-2ω0,则得到的信号是x(t)的正频谱分量的零中频信号：X+(f-f0)。两个正交的基带信号，也就是对应实部和虚部经过低通滤波得到的信号：
I(t)=[x(t)×cos(ω0t)]*hLP(t)
Q(t)=[x(t)×sin(ω0t)]*hLP(t)
I(t)和Q(t)都是实的基带信号，两谱相加或相减后，就变成了正负频率对称的实信号频谱了，其带宽为B/2,因此对于I(t)、Q(t)的采样速率只需要取为B，正交采样时候，采样率可以将为非正交采样时的一半。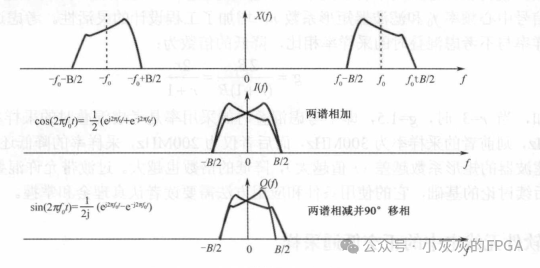

上面也就说明了，正交低通采样的最大好处就是可以降低采样率，而且还可以直接获得两个正交信号，有利于后续进行各种信号处理，当然也有一定的限制，需要一个正交混频器，如果正交混频做得不错，存在误差，就会影响正常工作。

相关内容 查看全部